越是简单的问题,解决起来越是复杂。越是复杂的问题,解决起来越是简单。
应用题的特征是:字数很多,数据也多,逻辑复杂。看起来好像难以入手,就像一个彪形大汉站在你面前,你不知上去以后如何动手。
但只要你掌握了窍门,抓住对方的弱点,放出一个大招,问题就迎刃而解了。
1、解决应用题的大招很简单,简单到只有四个字就能说出精髓:
等量关系
比如你去观察很多应用题的解题过程:上来就是列出一个或几个等式,然后再往下直接就计算出答案了。
对我们绝大部分的同学来说,计算谁不会啊?无非就是你计算的快一些,我计算的费点时间而已。区分我们的关键,就在于谁能列出最初的等式,而等式就是通过等量关系列出来的。
那等量关系的本质是什么?说穿了,也就是几个字:
你的东西=我的东西
那既然是:你的东西=我的东西,那这些东西的相等就必然是在同一个概念、同一个量级上的相等。
概念的相等,举例来说就是:吴彦祖的颜值=我的颜值(看咱这招黑体质!哎哎哎,后面那位童鞋,放下你手里的臭鸡蛋!)。你总不能拿吴彦祖的颜值和我的打字速度进行比较吧!
量级上的相等,自然就是单位上要统一,不能出现小时和分钟、千米和毫米,来进行比较了。
2、今天我们就拿应用题中的行程问题来做例子,让大家轻松找到等量关系。
行程问题中,基本上只涉及三个概念:路程,时间,速度。
既然只存在三个概念,那么行程问题中的等量关系,就只有三个:
路程=路程
时间=时间
速度=速度
纳尼?What are you 说啥嘞?别急,我举个简单的题,你就明白了。
两个人均从A地出发去B地,甲走路,速度3米/秒,乙骑车,10米/秒,
结果乙比甲提前半小时到达B地。求AB两地间距离。
这题其实很简单,你要是去问问你上小学的弟弟妹妹,他们也许口算就得出答案了,但我们这里是为了举例子不是?真题,要比这个复杂一些呢!
在这道题的题干的末尾(不是最后的求解部分),有这么一段话“结果乙比甲提前半小时到达B地”,这句话是什么意思?这句话就是在说“甲乙的时间差是半个小时”!
好了,等量关系冒头了,拿下!
甲的时间=乙的时间+半个小时
等量关系出来后,剩下的就是填充内容了。
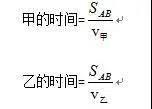
然后分别加入到等量关系中,基本框架就得出来了:
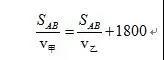
填入数字,就是最后解析上列出的式子了:
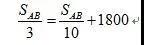
当然,这道题是简化了的模型,真题要比这个复杂一些,比如场景变一下、数据改动一下、出发时间有早有晚、中间车坏了要休息半小时等等。这些都是时间上的等量关系的依据,无非就是等式两边的数据多一些少一些而已,基本原则是不变的:时间=时间。
3、上面讲的简化模型太过简单,怕你怀疑老师的水平(其实老师水平也一般般啦!),我们就来一道真题来具体的练练手。看招:
某人开车从A地赶往B地,前一半路程比计划多用时45分钟,平均速度只有计划的80%,若后一半的平均速度为120km/h,此人还能按原定时间到达B地,A、B相距
A.450km B.480km C.520km D.540km E.600km
按照我们的原则,先看最后的描述:此人还能按原定时间到达B地。则等量关系为:
原计划用的时间=现在实际用的时间
填充内容:

则有:
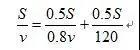
但是这道题,我们会发现,一个等式,有两个未知量,貌似不够啊。然后再细心观察这个式子,发现左右两边可以消掉S,求出v。不过我们的最终目的是求S,不是求出v。难道求出v,再代入这个式子求S吗?很明显,代入也是无法求出S的。
那就一定是我们少写了一个等式,如何检查是否少写了呢?最简单的办法就是:看还有哪些数据没有用上。
一看,还真找出来了:前一半路程比计划多用时45分钟。这个关系没有用上,那这个数据一定是另一个等量关系。
前一半路程计划使用时间=前一半路程实际使用时间—45分钟,接着补充内容:

组合到一起就是:
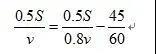
我们把列出的两个式子组合起来就是:
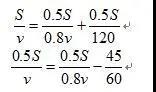
第一个式子得出v,代入到第二个式子,就可以算出S了。
以上是我们用“时间”上的等量关系来做题的,在行程问题中,还有“路程”、“速度”上的等量关系,不过“速度”用的很少,基本上“时间”和“路程”上的等量关系,就足够我们使用啦!
行程问题的解决思路基本上就是这些方法,它也是应用题中很重要的一类问题,其他方面的问题,限于篇幅,我们有时间再讲哈!
疫情期间,一定要做到:出门做好防护,在家做好消毒!我们下期再见!












 京公安网备11010802020593号
京公安网备11010802020593号