我们的同学应该都买过股票，在股票的交易中，有两个概念是相辅相成、缺一不可的，那就是估值和价值。我们常常用估值来代替公司的价值，估值估值，就是估算公司的价值嘛！

那我们也一定知道，估值是估算出来的，既然是估算，那就一定不是准确地描述价值。估值和价值是有偏离的，有的时候，估值高过价值，有的时候，估值低于价值。总的来说，估值是围绕着价值上下波动的。就像一个人牵着一条狗，狗有的时候走在主人前面，有的时候走在主人后面，但总归来说，是围绕着主人来回走动的。

对我们的学生来说，你真正学习到的内容，是你真正的价值。这个价值取决你平时背了多少单词，记了多少公式，做了多少道真题，刷了多少遍视频。而考试的成绩，是对你的一个估值，有的时候估值偏低，这时候不能气馁，觉得自己没有好好学习，或者觉得学习的知识没有用。你的价值没有变，你只是暂时性的估值偏低了。有的时候估值偏高，这时候不能骄傲，觉得自己已经超越了老师，后面不需要学习就能在考试中金榜题名。你的价值没有变，你只是暂时性的估值偏高了，你仍需踏踏实实地学习。

1

排列组合题中有一类题，经常性的是看了答案也看不懂，不知道答案讲的是啥。比如我们看其他排列组合题的答案，每一个数字都能对应上题中的已知条件。而这类题的答案中，有些数字都不知道怎么来的，题中的已知条件中，有些数字居然好像没用上。下面我们来瞅瞅这到底是何方妖孽！看题：

某校准备参加全国高中数学联赛，把10个名额分配给高三年级5个班，每班至少1人，则不同的分配方案有（）

A,84种      B,126种      C,756种

D,210种    E,64种

这道题倒是类似于我们以前学过的分组问题，也是“僧多粥少”、“狼多肉少”的状态。但有一点不同的地方是，分组问题中，要分的元素都是不同的，比如把5个医生分配到4所医院这类。而这道题中，由于名额都是相同的，所以不同的分配方案在于，每个班分到名额的个数不同。那像这类题怎么做呢？我们用传说中密不外传的——“隔板法”。

我们把10个名额排成一排，10个名额的中间形成了9个可用的空当。那我们要想把这10个名额分成5组，就需要我们在这9个空当中插入4块隔板，这4块隔板就把这10个名额分成了5部分，这5部分对应着5个班级。答案即：

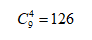
你看，题中出现了10和5，答案中出现了9和4，这都是猛一看扯不上啥关系的数字。你说你只看答案能看得懂么？

我们来总结一下这类题的规律：对于元素全部相同的情况，我们就用隔板法来求解。隔板法的做法是看总有有多少个相同的元素，中间形成了多少个空，要求隔成几组，需要多少块隔板。

2

隔板法比较简单一些，适用于相同元素的分组分配问题。还有一种问题，要求几个元素不相邻，比如几个人坐在一排座位上，要求人与人之间不能相邻，或者每个人左右两边都有空位等问题。我们来看一道具体的题：

3个人坐在一排8个座位上，若每人的两边都要有空位，则不同的坐法有多少种？

A,12     B,24     C,36     D,48    E,60

像这类每个人都不能相邻的问题，我们称之为不相邻问题。这类问题，我们往往是先其他后特殊。

这里和我们做其他排列组合题的顺序相反，我们在做一般的排列组合题的时候，都是先特殊后一般。先把特殊要求的元素安排好。再去安排普通的元素。（会议落座的时候，不得先安排领导，再安排咱们小兵么？对不？一样的道理）。而在这里，我们要反其道而行之，先一般后特殊。

由于第一个座位和最后一个座位不能坐人（坐了就不再是左右两边都是空位啦），所以这3个人只能去坐中间的6个座位。那这道题就变成了，3个人坐6个座位，然后互相之间不相邻的问题了。要想不相邻，任意两个人中间得有空位。那我们把这三个人塞入空位子之间不就可以了么，你在两个空板凳中间，你左右两边自然就没人了嘛？（老师，那难道要我在两个椅子中间蹲着吗？傻孩子，你搬个凳子坐在两个空凳子中间啊）。

6个座位，这三个人从中间搬走3个凳子（这是他们要坐的凳子），还剩下三个空凳子，这三个空凳子的左右两边和中间，共有4个空挡。我们把这三个带着凳子的人，塞入这四个空当中，不就实现了每个人左右两边都有空座位了么？然后这三个人坐的顺序再来个阶乘，所以答案就是：

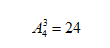
3

接着上面的插空法，我们再来一道题，练练手：

5个成人带领2个小孩排队上山，小孩不排在一起也不排在头尾，则不同的排法有

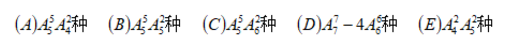
首先我们先排小孩子，这两孩子不排在一起，也不排在头尾，那意思就是这两孩子每个人左右两边都有空位呗，和上面的那道题就类似了。那我们先除掉前后两个位置，因为俩孩子不能在这里排。这俩孩子要在中间的5个位置中，占据两个位置，而且这俩孩子还不能挨着，那我们让这俩孩子带走两个位置在旁边旁观，剩余了3个位置，这三个位置，左右两边和中间共计是4个位置，只要这两孩子带着位置插入这4个空位中，就能实现俩孩子不挨着，也不在排头和排位。同时，俩孩子的前后顺序也有一个阶乘。那就是：

我们看下答案，有这个么？没有，那我们忽略了谁？我们只顾着安排孩子，忘了安排5个大人了。这5个大人在剩余的5个位置上还可以随便排列，那这个题的答案就应该是：

除了上述两道题以外，我们还有比如说：每个人左边都是空位、右边都是空位、或者仅仅是每个人都不挨着（即排头排尾能坐人）等等，我们可以根据具体的题目，来增加减少空位的数量，再解出答案。

我们来总结一下，插空法的原则：先其他后特殊，即排除要求不相邻的元素，先把剩下的其他元素排好位置，形成若干个空位，再把要求不相邻的元素插入这些空位中。

好了，隔板法和插空法我们就讲到这里了。考试就算考到，也是很简单的，所以大家把上面的内容好好掌握就好了。欢迎大家点赞收藏关注，我们下期再见！