有句话我们大家都很熟悉：听过很多大道理，却仍然过不好这一生。于是乎，有人觉得原因是出在这些“大道理”上，是这些“大道理”的道理还不够深刻，所以没有改变我们的命运，没有让我们过好这一生。

但是，越是活的成功，越是活的通透的人，在他们眼里，他们活的就是那些简单的“大道理”。那同样是“大道理”，为什么有的人能够活的很成功，而另一些人活的浑浑噩噩呢？答案就在于两个字：

践行

一切道理靠践行，一切的成功，也都靠践行。只是嘴上说的过瘾，如果没有真正的沉下身子去老老实实的去执行，是万不可能成功的。

有个笑话是这样讲的：一个人天天虔诚地向上帝祈祷：主啊，让我彩票中奖500万吧！每天如此，每天如此。坚持了很多天后，有一天，上帝终于降临在他面前。只见上帝怒气冲冲地对他说：你TM的倒是去买张彩票啊！

所以，在我们考研的历程中，真的没有什么捷径，真的没有什么窍门。有的就是老老实实的看书，学习和做题，有的就是每天熬夜看书的痛苦，有的就是每天坚持早起背过的单词，有的就是受到打击后仍然认为自己能考上的信心。。。。。。

这世间充斥着很多“大道理”，认真的去对待这些朴素的道理，认真的在生活工作中，实践这些道理，那些最终获得的成功，在你看来，就是这些道理“生效”了。而“大道理”只是听过，而没有严格地，不折不扣地，执拗地去执行，那持续的原地踏步，在你看来，就是这些道理“没有用”，那你再去寻找什么“更没用”的窍门，又怎么能成功呢？

1

绝对值在我们的考试中还是占据有一定的分量的，虽然考的不算很多，但是在很多题中都有体现。今天我们来看一种绝对值中比较偏难一些的题。我们争取能在这篇文章中给大家讲清楚这类题的背后原理，做题技巧。来，上题：

如果关于x的不等式|3-x|+|x-2|<a的解集是空集，则a的取值范围是

A,a<1     B,a≤1     C,a>1     D,a≥1     E,a≠1

这道题正常的做法，就是先将y=|3-x|+|x-2|的图像画出来，然后根据图像和y=a相交的情况，来最终判断a的范围。

我们先来用正常方法做一遍，然后总结一个规律。首先我们将y=|3-x|+|x-2|写成分段函数：

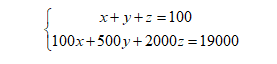
接着我们画出该函数在坐标轴中的简图：

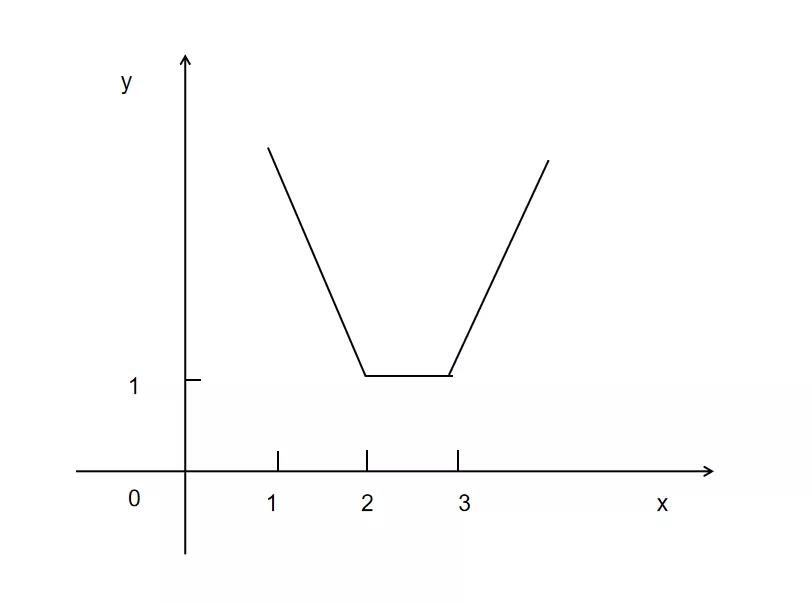
你看看，形状像不像灰太狼的平底锅呢？我们把这个图形称为平底锅模型。

然后题中说，函数的值小于a的解集是空集，意思是啥？就是不能小于a呗！不能小于a，啥意思呢？就是大于等于a永远成立呗。那啥叫做永远大于等于a呢，怎么才能永远才能大于等于a呢？只有最小值都大于等于a，才能保证我永远大于等于a啊！

举个例子：李老师的财富<马云的财富是假的（可以理解成是空集），那就是李老师我的财富要≥马云的财富永远成立呗，那我怎么保证我的财富永远大于等于马云财富呢，就是我财富最低的值，都大于等于马云的财富，才能说我永远大于等于马云的财富啊！！！（哎哎哎，放下你们手中49米长的大刀）。

那这道题的关键就在于求解出函数y=|3-x|+|x-2|的最小值，根据图形，我们知道，最小值是1，那就是1大于等于a，即a≤1。这就是答案了。

那能不能再简单一些，我们能不能不画图，就找出这类函数的最小值呢？

当然可以啦，类似于y=|3-x|+|x-2|的函数，两个绝对值中间是+号的，只有最小值，没有最大值。最小值是两个零点的差的绝对值。什么是零点呢，就是我们令绝对值内部等于0，得出来的x的值。比如这个函数y=|3-x|+|x-2|的两个零点是3和2，那3和2的差是±1，其中的正1就是函数的最小值（为啥不是-1，因为两个绝对值相加，不可能是负数啊！）

所以类似于y=|x-a|+|x-b|的最小值就是两个零点的差，要正的那个，即|a-b|！

2

我们再来两道同类型的题，练练手：

不等式|x-2|+|4-x|<s无解.

（1）s≤2.     （2）s>2.

首先我们判断函数y=|x-2|+|4-x|的最小值，两个零点是2和4，最小值是4-2=2，图形是平底锅模型。|x-2|+|4-x|<s无解，也就是空集的意思，就是|x-2|+|4-x|不能小于s呗，那就是|x-2|+|4-x|≥s恒成立喽，那就是2≥s喽。条件（1）充分，选A。

方程|x+2|+|x-8|=a有无数正根.

（1）-4<a<4.     （2）a=4.

首先我们判断函数y=|x+2|+|x-8|的最小值，两个零点是-2和8，最小值是8-(-2)=10，图形是平底锅模型。方程|x+2|+|x-8|=a有无数正根，说明函数y=|x+2|+|x-8|和函数y=a有无数个交点啊，那就是函数y=a的图像和函数y=|x+2|+|x-8|的图像有某条线重合啊！那就只能是和平底锅的底重合了（y=a平行于x轴，只能和底重合）。重合就是值相等。所以a就是函数y=|x+2|+|x-8|的最小值，即a=10。这道题选E喽。

3

那有同学会问了，老师，上面的都是两个绝对值相加的形式，有没有两个绝对值相减的形式呢？当然有了，看题：

若不等式|x+3|-|x-6|>a有解，则a的取值范围是

A,a>-9   B,a≤-9   C,a≤9   D,a<9   E,a>9

这类题的图形画出来是个Z字型或者反Z字型（这里要求你自己在图上画一下，验证一下）。不过具体是Z字型还是反Z字型都无关紧要，我们关心的是最大值和最小值。

那像这类两个绝对值相减的类型，它是有最大值和最小值的。如何确定两个最值的大小呢？首先，找零点，-3和6。其次，作差，两个零点的差，-9和9。好了，-9就是最小值。9就是最大值。So easy！

|x+3|-|x-6|>a有解，意思就是不管a咋样蹦跶，我都能大于你，意思就是我只需要保证我的最大值能大于你就ok了。最大值是9，那就是9>a，即a<9了。选D。

好了，上面是我们用比较简单的形式讲解了这类题的做法，我们下面给出通用的模型总结，大家要记好呀！

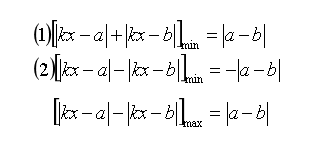
好了，我们这期的内容就讲到这里啦。感谢大家观看，欢迎大家点赞收藏点在看。威廉詹姆斯说过：人类本质中最殷切的需求，是渴望得到他人的肯定。您的支持，是我持续输出优质内容的动力！我们下期再见！