人不可追求百分之百的安全感。百分之百的安全，带来的是百分之百的束缚。不学会抛弃一部分，就没有机会和他人合作。不选择放弃一部分，也就谈不上对别人的信任。

任何考试如果不设置一个期限，而是等到你准备好了再去考，估计大部分人都会以自己没准备好为由，一再拖延不去考试。这就好比走路的时候，如果想要百分百的安全感，就永远迈不出第一步，因为你满脑子想的都是该迈哪一条腿更安全。

进步的前提是你敢于迈出第一步，而不是总在担心，自己这一步迈得漂不漂亮。害怕被嘲笑的人，更有可能成为“表现型人格”，过分关注别人的评价，通常是为自己进步挖的坑。其实过分在意别人的眼光，归根到底是因为没有想清楚这两件事的重要等级：别人眼中的“好形象”带来的满足感与自身进步带来的满足感。

过度追求每一步都在自己的可控范围内，是不敢开始的最大障碍。拖延症也好，完美主义也好，大部分人不愿意接受这个现实：没有人能够一开始就做好。所以，大胆迈出第一步，就已经成功了一半。

1

我们在上一期的内容中，讲过一道只提供了时间的数据的题，今天我们来看一道，只提供了速度的数据，时间的数据比较模糊的题。

（2001年）某人下午三点钟出门赴约，

若他每分钟走60米，会迟到5分钟，

若他每分钟走75米，会提前4分钟到达，

则所定的约会时间是下午（）

A，三点五十分  B，三点四十分  C，三点三十五分  D，三点半

只要是做行程问题，就一定要把路程、时间、速度考虑进去，如果题中没有给数据或者没有提，那我们也要假设一个出来。

路程我们可以假设为S。那么时间呢？直接用迟到5分钟，早到4分钟表示么？肯定不是的，不过这里我们注意到，迟到和早到是有一个衡量标准的，那就是准点的那个时间点，那我们假设正好卡着时间点到的时间（若是一个男的卡着点赴约，我估计这哥们现在还单着呢），距离三点的时间是t分钟。那么迟到五分钟，就是用时t+5分钟；早到四分钟，就是用时t-4分钟。根据题意有：

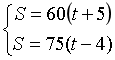
容易解得t=40分钟，也就是该小伙子赴约时间是三点四十分（这个点约会是不是有点尴尬，肯定是为了省饭钱！哈哈！）。

2

行程问题中，除了单纯给了时间数据的题型以外，还有单纯给了速度的数据和单纯给了路程的数据的问题。我们分别来看一下。

（2006年）某人以6千米/小时的平均速度上山，

上山后立即以12千米/时的平均速度原路返回。

那么此人在往返过程中的每小时平均所走的千米数为（）

A，9     B，8     C，7     D，6     E，以上均不对

只给了两个速度的数据，最终求的也是速度（平均速度）。还是老办法，该咋办咋办。求平均速度，就需要总路程和总时间。我们假设上山路程为S，因为原路返回，所以总路程为2S。时间上分为两段，第一段是上山时间，第二段是下山时间。则总时间有：

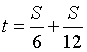
因此，所求的平均速度为：

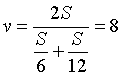
完美解决！然后我们再来看一道，只提供路程的数据的题型。

（2007年）甲、乙、丙三人进行百米赛跑（假设他们的速度不变），

甲到达终点时，乙距终点还差10米，丙距终点还差16米。

那么乙到达终点时，丙距终点还有（）米。

A，22/3     B，20/3     C，15/3     D，10/3  E，以上均不对

还是那个原则，路程、速度、时间都安排上。第一段，甲到达终点时，乙距终点还差10米，丙距终点还差16米。意思就是：同样时间，甲跑100米，乙90米，丙84米。根据时间相等的等量关系，可得：

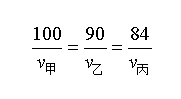
第二段，乙到达了终点（甲估计这会儿已经冲到了主席台），假设这时候丙距离终点为x，那么同样的时间，乙跑了100，丙跑了100-x，根据时间相等的等量关系，可得：

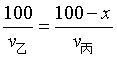
上面两式结合，就可以求得：x=20/3米。看来丙要加强身体锻炼呀！发现没有，这里其实没有甲什么事儿，甲虽然当了冠军，但也没起到啥作用哦！

3

最后我们来看一道正常的行程问题，这道题因为比较绕一些，所以很多学生都问过这道题。问的多，就说明这道题还是有代表性的，值得我们好好研究研究。

（2009年）一艘小轮船上午8点起逆流而上（设船速和水流一定），

中途船上一块木板落入水中，直到8点50分，

船员才发现这块重要木板丢失，立即调转船头去追，

最终于9点20分追上木板。由上述数据可以算出木板落水的时间是（）

A，8:35     B，8:30     C，8:25     D，8:20  E，8:15

我们来画一个简图。

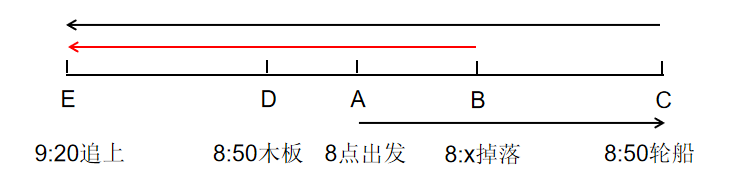
简单描述一下过程：

①8点从A点逆水向右出发；

②8:X在B点，木板掉落向左漂流，轮船继续逆行向右；

③8:50轮船到达C点，发现情况，调转船头，此时我们假设木板到达D点。

④9:20，轮船追上木板。

其实撇去前面的过程，这道题就是一道追及问题。追及问题中，轮船和木板的速度都有了，追上的时间也有了（8:50到9:20，共追了30分钟）。差一个什么呢？差一个他们开始追的时候，相距的距离。在图上表示，就是CD的距离。所以这道题的关键就是求CD的距离。

CD怎么求呢？CD可以分为两部分，BC和BD。

BC是轮船走了50-X分钟（8:X到8:50）走的路程，速度是船速减水速。

BD是木板漂了50-X分钟（8:X到8:50）走的路程，速度是水速。

据此，CD长度可以表示为：

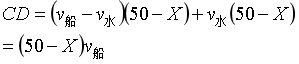
那根据追及问题的模型，船从C追了30分钟（8:50到9:20）追到了E。木板从D漂了30分钟（8:50到9:20）漂到了E。有：

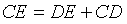
分别代入数据和表达式，为：

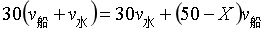
易得，X=20，也就是8:20木板落的水。

好了，这期的内容，我们就讲到这里了，希望每期的内容都能对大家的考研之路，起到一点点的帮助，我们下期再见！